
After having detailed multi-objective voyage optimisation as a concept and framework, our series comes to its final piece with breaking down and understanding the operational differences between a single-objective voyage optimisation and the more advanced multi-objective solution.
Voyage optimisation has undoubtedly evolved into a multi-objective issue over time. This is due to the complex nature of the operations that need to simultaneously consider a suite of variables and balance them to reach best results. Thus, in our first blogpost you can find here we have concluded that traditional single-objective voyage optimisation approach fails to efficiently tackle today’s multi-objective tasks.
As the single-objective algorithm focuses solely on one objective, such as minimising fuel consumption, crucial variables are often overlooked during the optimisation process. This can lead to a final solution that prioritises one objective (such as fuel efficiency) while neglecting other important factors such as voyage duration or just-in-time arrival.
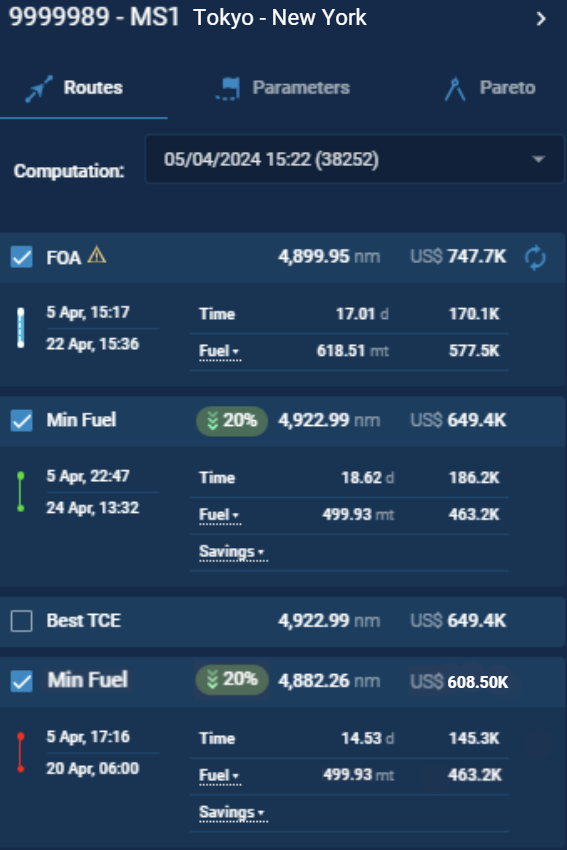
Let’s evaluate two potential routes that consume the same amount of fuel, 500 metric tons (mt), but have different voyage durations: one lasting 450 hours and the other approximately 350 hours. A single-objective approach would treat these routes equal since only fuel consumption is factored into the decision-making process. Therefore, the ultimate decision between these routes would lack a clear basis, even though one of them leads to a better outcome.
To address previously detailed issue, a commonly employed method by single-objective optimisations involves the utilisation of a weight-vector technique. This method simplifies a multi-objective problem by assigning weights to each objective, creating a single quality indicator. However, this approach has its own challenges. It demands extensive fine-tuning and a thorough grasp of the problem's structure within the search space. Acquiring such insight is difficult and often requires solving the problem multiple times. Additionally, since each problem is unique, the fine-tuning process must be repeated for each scenario, as no single set of weights can perfectly accommodate all situations. Consequently, this leads to suboptimal solutions, particularly when dealing with an increasing number of objectives.
In single-objective optimisation, you only get one solution, and running the optimisation again is unlikely to provide a different result. But the results of these computations do not not consider what owners, charterers, captains, or other important decision-makers prefer.
On the other hand, multi-objective optimisation offers a variety of optimised routes known as the Pareto Optimal Front. Each route can be assessed separately, giving decision-makers the flexibility to select the most appropriate voyage, even if it doesn't excel in every aspect like fuel consumption, ETDS or ETAs, voyage time, TCE, etc. Moreover, multi-objective solutions maintain high accuracy and efficiency regardless of route length and complexity.
Finally, a Multi-Objective Algorithm is both scalable and future-proof because it's easy to include more objectives in the process. This ensures that the algorithm remains adaptable to evolving needs and can continue to effectively optimise complex decision-making scenarios.
We have analysed the differences between single-objective and multi-objective approaches. Single-objective methods often overlook important variables, leading to less accurate results. To compensate, they employ weight-vector techniques, which require extensive fine-tuning and struggle with complex scenarios. In contrast, multi-objective optimisation offers a range of optimised routes, known as the Pareto Optimal Front, providing decision-makers with flexibility and ensuring high accuracy and efficiency regardless of route complexities. Multi-objective algorithms are scalable and adaptable, making them robust solutions for modern maritime operations.